Newton Raphson Method

The Newton-Raphson method for finding the roots of a function makes use of the gradient.

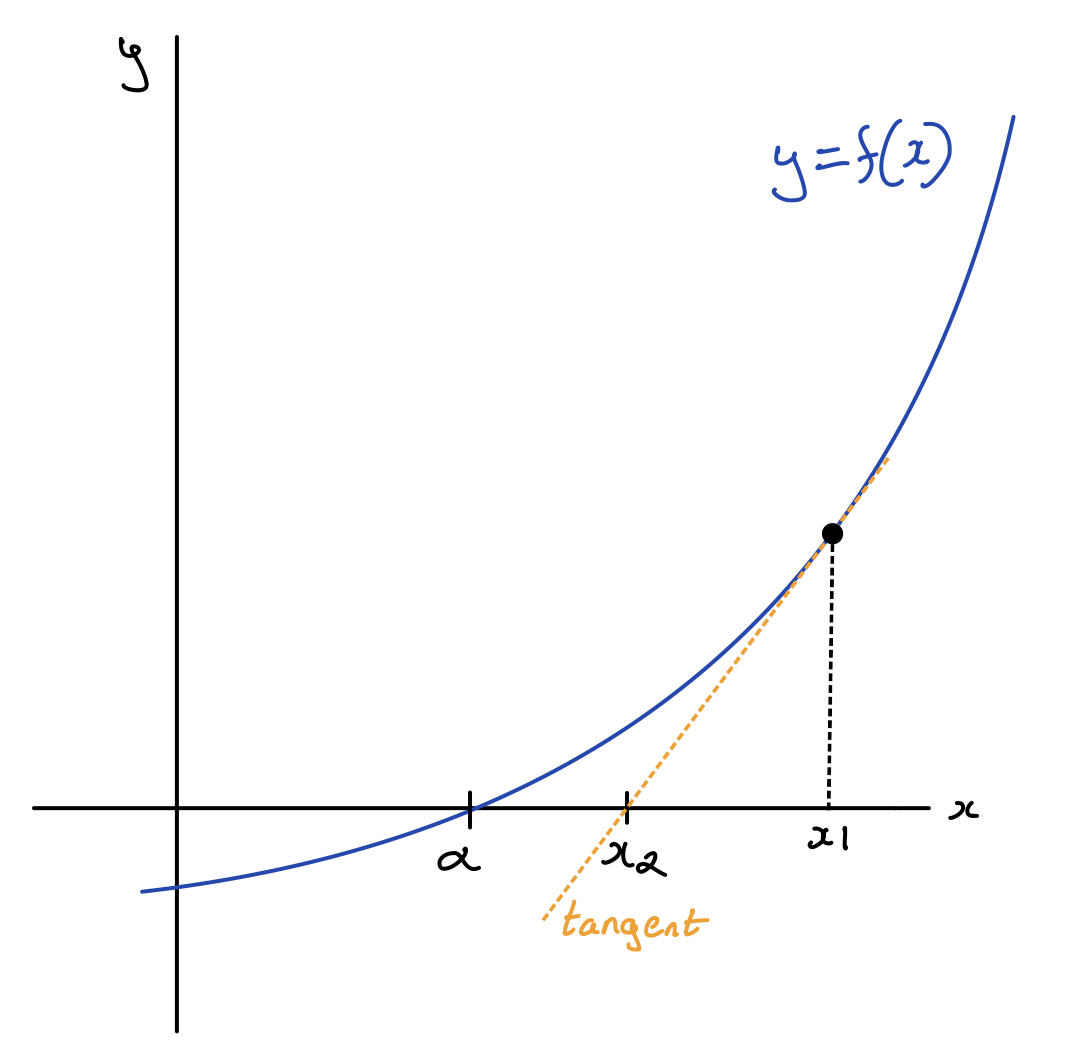
Figure 5 below shows a function $y=f(x)$ which has a root at $x=α.$ $x_1$ is an initial approximation to this root. A better approximation to the root can be found by using the tangent to the function at $x=x$. The location where the tangent intercepts the $x$-axis, $x_2$ is closer to the root than $x_1$.

We can find an expression for $x_2$ by considering the equation of the tangent. The tangent has gradient $f^\prime(x)$, and meets the curve at $(x,f(x))$. Hence, using the formula $y−y_1 = m(x−x_1)$, the equation of the tangent at $x_1$ is

$x_2$ is the location where the tangent intercepts the $x$-axis $(y=0)$. Therefore,

Rearranging to give an expression for $x_2$,

This procedure can be repeated to find better approximations to the root by turning the equation above into an iterative sequence,

What are the limitations of this method?

There are situations in which the Newton-Raphson method will not find the root of a function.

1. Using the Newton-Raphson method may produce a value of $x_r$ which is outside the domain for which the function is defined. If this occurs, it is not possible to find further values of $f(x_r)$ or $f^\prime(x_r)$ and get back to the root, so the method fails completely.This is illustrated in NUMBER below. The function $y = f(x)$ is defined for $[a,b]$. Using the Newton-Raphson method starting at $x_1$ gives a value for $x_2$ that is outside the interval $[a,b]$.

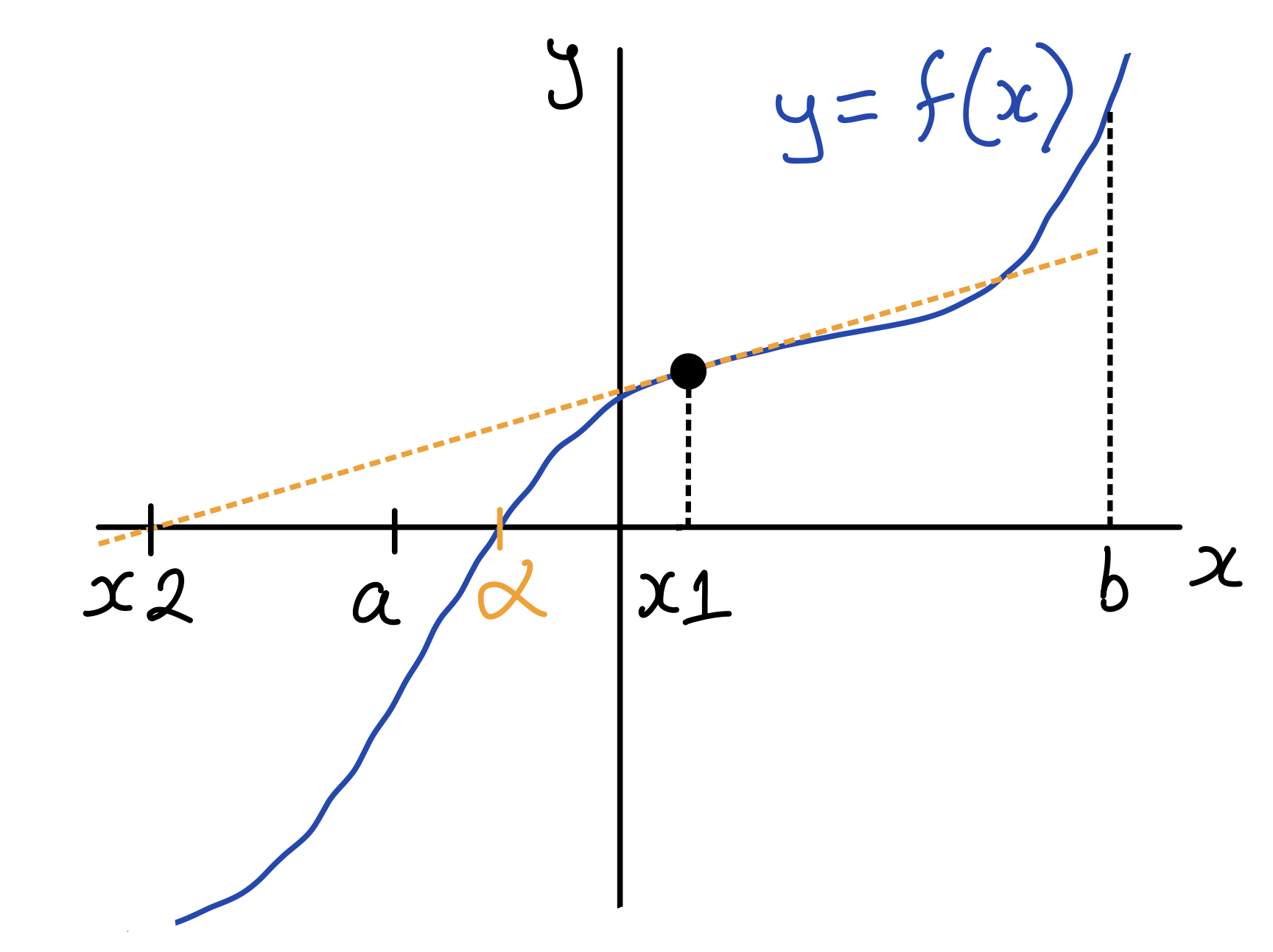A case where the Newton-Raphson method fails: $x_2$ is outside the domain of $f(x)$.

2.

Algorithm

Below is the pesudocode for the algorithm that implements Newton Raphson.

INPUT initial approximation po; tolerance TOL; maximum number of iterations No.
OUTPUT approximate solution p or message of failure.
Step 1 Set i = 1.
Step 2 While i ≤ No do Steps 3-6.
    Step 3 Set p = po - f(po)/f'(po). (Compute pi.)
    Step 4 If |p =po| < TOL then
        OUTPUT (p); (The procedure was successful.)
        STOP.
    Step 5 Set i = i +1.
    Step 6 Set po = p. (Update ро.)
Step 7 OUTPUT ('The method failed after No iterations, No =', No);
(The procedure was unsuccessful.)
STOP.

In Python you can do this with

import numpy as np
x = np.linspace(0, 10, 100)
print(x[:5])